Počty (n500)

[ TOP | << | < | > ] Poslední úprava 2023-11-11 22:19. notýsek elektronika ▪MathML

Počty

Dekadické předpony násobků a zlomků

Viz též Předpona soustavy SI - Wikipedie, otevřená encyklopedie.

Předpony dekadických násobků jednotek.
název	zkratka	velikost		dlouhý systém	krátký systém
exa	E	10¹⁸	1 000 000 000 000 000 000	triliarda	quintillion
peta	P	10¹⁵	1 000 000 000 000 000	biliarda	quadrillion
tera	T	10¹²	1 000 000 000 000	bilion	trillion
giga	G	10⁹	1 000 000 000	miliarda	billion
mega	M	10⁶	1 000 000	milion	million
kilo	k	10³	1 000	tisíc	tisíc (mille)
hekto	h	10²	100	sto
deka	da	10¹	10	deset

Předpony dekadických zlomků jednotek.
název	zkratka	velikost
deci	d	10⁻¹	0,1	desetina
centi	c	10⁻²	0,01	setina
mili	m	10⁻³	0,001	tisícina
mikro	µ	10⁻⁶	0,000 001	milióntina
nano	n	10⁻⁹	0,000 000 001
piko	p	10⁻¹²	0,000 000 000 001
femto	f	10⁻¹⁵	0,000 000 000 000 001
atto	a	10⁻¹⁸	0,000 000 000 000 000 001

Seznam čísel, Krátká a dlouhá škála.

Jednotky informace a jejich násobky

Předpony binárních násobků jednotek.
název	zkratka	velikost
exa binary	Ei	2⁶⁰	1 152 921 504 606 846 976
peta binary	Pi	2⁵⁰	1 125 899 906 842 624
tera binary	Ti	2⁴⁰	1 099 511 627 776
giga binary	Gi	2³⁰	1 073 741 824
mega binary	Mi	2²⁰	1 048 576
kilo binary	Ki	2¹⁰	1 024

U počítačů se užívají i binární násobky jednotek informace a v praxi užívané zkratky jsou dosti nepřehledné i navzdory již mnoho let zavedeným normám například:

IEC 60027-2: Letter symbols to be used in electrical technology - Part 2: Telecommunications and electronics;
IEEE 1541 is a standard concerning the use of prefixes for binary multiples of units of measurement related to digital electronics and computing;

Nejasnosti jsou i kolem jednotek vyjadřující množství informace. Viz. též Byte - Wikipedie, otevřená encyklopedie.

Jednotky informace.
popis	název	zkratka
dvojková číslice, binary digit	bit	b (bit)
slabika, bajt, byte ; většinou délky 8 bitů	byte	B (b)
oktet = slabika o osmi bitech	octet	o

Řady standardních hodnot

Procentní řada je řada hodnot o n členech. Každý člen má toleranční pole stejně široké o velikosti 1/n. Poměr mezi sousedními členy řady je konstantní a má hodnotu ⁿ√10 (n-tá odmocnina z deseti). Hodnota i-tého členu z řady o n prvcích je 10^(i/n). Norma IEC 60063 Preferred number series for resistors and capacitors.

Řady standardních hodnot procentní řady
řada	tolerance	hodnoty
E3		1,0								2,2								4,7
E6	±20 %	1,0				1,5				2,2				3,3				4,7				6,8
E12	±10 %	1,0		1,2		1,5		1,8		2,2		2,7		3,3		3,9		4,7		5,6		6,8		8,2
E24	±5 %	1,0	1,1	1,2	1,3	1,5	1,6	1,8	2,0	2,2	2,4	2,7	3,0	3,3	3,6	3,9	4,3	4,7	5,1	5,6	6,2	6,8	7,2	8,2	9,1

Řada E48 v toleranci ±2 %, řada E96 v toleranci ±1 %, řada E192 v toleranci ±0,5 %. Viz též písmenový kód pro dovolené úchylky součástek výrobce TESLA. Článek „Jak získat neobvyklé hodnoty odporů a kondenzátorů?“ v rubrice Jak na to časopisu Amatérské rádio číslo 9, ročník 1970, strany 326 a 327, obsahuje tabulky vypočítaných hodnot kombinací prvků.

Renardova řada, aproximuje exponenciálu, ISO 3. Často použitá na strojní díly (např. délka hřebíku), na konstantu A_L (Λ) u jader magnetických obvodů. Pasívní součastky firmy TESLA n.p. kolem roku 1950.

Řady standardních hodnot Renardovi řady
řada	hodnoty
R5	1,00				1,60				2,50				4,00				6,30
R10	1,00		1,25		1,60		2,00		2,50		3,15		4,00		5,00		6,30		8,00
R20	1,00	1,12	1,25	1,40	1,60	1,80	2,00	2,24	2,50	2,80	3,15	3,55	4,00	4,50	5,00	5,60	6,30	7,10	8,00	9,00

Funkce ostrého úhlu

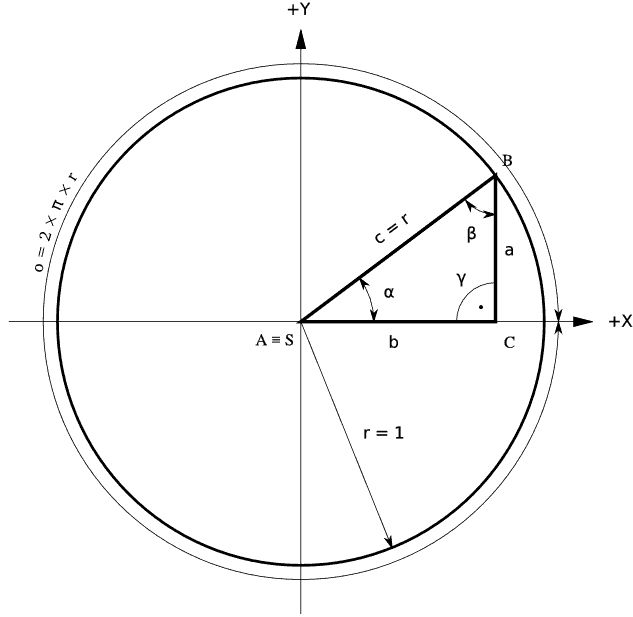
V pravoúhlém trojúhelníku platí: $\sin α = \frac{a}{c} = \frac{protilehlá}{přeponě}$ $\cos α = \frac{b}{c} = \frac{přilehlá}{přeponě}$ $tg α = \frac{a}{b} = \frac{protilehlá}{přilehlé}$ $cotg α = \frac{b}{a} = \frac{1}{tg α} = \frac{přilehlá}{protilehlé}$

Úhel γ = 90°. Součet vnitřních úhlů trojúhelníka v euklidovské rovině je roven 180°; platí α + β + γ = 180° .

Pythagorova věta: plocha čtverce nad přeponou se rovná součtu ploch čtverců nad odvěsnami, vztah je c² = a² + b² .

Na stránkách Wikipedie článek Trojúhelník.

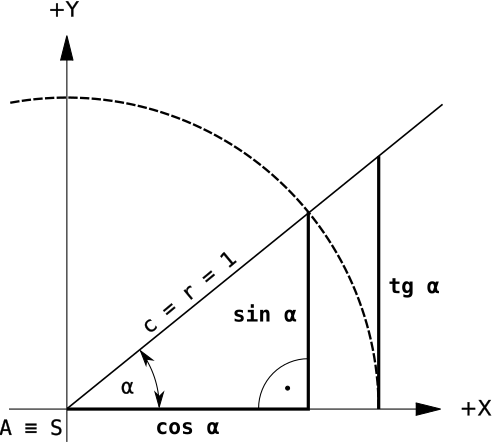
sin α	0°	30°	45°	60°	90°
sin α	$\sqrt{\frac{0}{4}} = 0$	$\sqrt{\frac{1}{4}} = 0,5$	$\sqrt{\frac{2}{4}} \approx 0,707$	$\sqrt{\frac{3}{4}} \approx 0,866$	$\sqrt{\frac{4}{4}} = 1$	cos α
	90°	60°	45°	30°	0°	cos α

Goniometrické funkce

Řecká abeceda

Řecká abeceda.
písmeno		ISO 8879	ISO 10646	LATEX	písmeno		ISO 8879	ISO 10646	LATEX	písmeno		ISO 8879	ISO 10646	LATEX
alfa	α	α	U+03B1	\alpha	iota	ι	ι	U+03B9	-	ró	ρ	ρ	U+03C1	-
alfa	Α	Α	U+0391	-	iota	Ι	Ι	U+0399	-	ró	Ρ	Ρ	U+03A1	-
beta	β	β	U+03B2	\beta	kappa	κ	κ	U+03BA	-	sigma	σ	σ	U+03C3	-
beta	Β	Β	U+0392	-	kappa	Κ	Κ	U+039A	-	sigma	Σ	Σ	U+03A3	-
gama	γ	γ	U+03B3	\gamma	lambda	λ	λ	U+03BB	\lambda	tau	τ	τ	U+03C4	-
gama	Γ	Γ	U+0393	-	lambda	Λ	Λ	U+039B	-	tau	Τ	Τ	U+03A4	-
delta	δ	δ	U+03B4	-	mí	μ	μ	U+03BC	-	ypsilon	υ	υ	U+03C5	-
delta	Δ	Δ	U+0394	-	mí	Μ	Μ	U+039C	-	ypsilon	Υ	Υ	U+03A5	-
epsilon	ε	ε	U+03B5	-	ný	ν	ν	U+03BD	-	fí	φ	φ	U+03C6	\varphi
epsilon	Ε	Ε	U+0395	-	ný	Ν	Ν	U+039D	-	fí	Φ	Φ	U+03A6	\phi
dzéta	ζ	ζ	U+03B6	-	ksí	ξ	ξ	U+03BE	-	chí	χ	χ	U+03C7	-
dzéta	Ζ	Ζ	U+0396	-	ksí	Ξ	Ξ	U+039E	-	chí	Χ	Χ	U+03A7	-
éta	η	η	U+03B7	-	omikron	ο	ο	U+03BF	-	psí	ψ	ψ	U+03C8	-
éta	Η	Η	U+0397	-	omikron	Ο	Ο	U+039F	-	psí	Ψ	Ψ	U+03A8	-
theta	θ	θ	U+03B8	-	pí	π	π	U+03C0	-	omega	ω	ω	U+03C9	\omega
theta	Θ	Θ	U+0398	-	pí	Π	Π	U+03A0	-	omega	Ω	Ω	U+03A9	\Omega

Symbol theta = ϑ (&thetasym; , U+03D1 , \vartheta), symbol kappa = ϰ (U+03F0), symbol rhó = ϱ (U+03F1 , \varrho ).
Greek Symbols Character Entities (%isogrk3;), The Unicode Consortium: Home Page. Fí. Matematické symboly a značky – Wikipedie.

Průměr

Aritmetický průměr (ve statistice charakteristika polohy hodnot znaku) tzn. součet všech hodnot vydělený jejich počtem.

\bar{x} = \frac{x_{1} + x_{2} + \dots + x_{n}}{n}

Slouží k výpočtu střední hodnoty střídavého proudu (stejný náboj, stejné elektrolytické účinky, Q ∼ I). V aplikačních programech tabulkový kalkulátor realizováno funkcí: gnumeric 1.8.2: AVERAGE(value1, value2,...); sc 7.16: @avg(r); OpenOffice.org 3.0.1 Calc: AVERAGE(číslo 1, číslo 2, ...). 1 Average Voltage of a Sinusoidal AC Waveform.

Kvadratický průměr je statistická veličina (ve statistice charakteristika variability neboli rozptýlení hodnot znaku) představující druhou odmocninu aritmetického průměru druhých mocnin daných hodnot.

s = \sqrt{\frac{{x_{1}}^{2} + {x_{2}}^{2} + \dots + {x_{n}}^{2}}{n}}

Výsledek kvadratického průměru je nezáporné číslo. Slouží k výpočtu efektivní hodnoty (anglicky root-mean-square value = česky odmocnina průměru čtverců) střídavého proudu (stejná práce, stejné tepelné účinky, W ∼ I²). V aplikačních programech tabulkový kalkulátor lze použít funkci: gnumeric 1.8.2: STDEV(b1, b2, ...); sc 7.16: @stddev(r). RMS Voltage of a Sinusoidal AC Waveform.

Matematika zná i další průměry např. Vážený průměr – Wikipedie, Geometrický průměr – Wikipedie, Harmonický průměr – Wikipedie, viz Nerovnosti mezi průměry – Wikipedie a Průměr aritmetický, vážený, geometrický, harmonický, Teorie čísel ve starém Řecku - BPTX_2011_1_11320_0_236860_0_114606.pdf. Nerovnosti mezi průměry – Wikipedie. Určitá vstupní řada dat je nahrazena jedinou hodnotou, tedy "nějakým průměrem". To jaký to bude průměr, záleží na tom, jak je ve výrazu použit: a + Σ aritmetický; krát × Π geometrický; + krát sám sebou x² kvadratický; za 1/x = x⁻¹ harmonický.

Mocniny a odmocniny

Počítání s mocninami:

součin mocnin stejného základu		$a^{m} \cdot a^{n} = a^{m + n}$
krácení zlomku		$\frac{a^{m}}{a^{n}} = a^{m - n}$
mocnina mocniny		$a^{m^{n}} = a^{m \cdot n}$
součin mocnin stejného exponentu		$a^{m} \cdot b^{m} = {(a \cdot b)}^{m}$

Počítání s odmocninami:

		$\sqrt[n]{a} = a^{\frac{1}{n}}$
odmocnina součinu		$\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}$
odmocnina podílu		$\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$
odmocnina odmocniny		$\sqrt[n]{\sqrt[m]{a}} = \sqrt[n \cdot m]{a}$

Jiří Holčík , dokument Signály, časové řady a lineární systémy.

Literatura

Zdroje informací, které stojí za to:

[1]	Internet, Matematika pro střední a základní školy — Matematika.cz.
[2]	Internet, Mapa matematiky. Je veskrze dobré „znát mapu“. Tato je sice anglicky, ale s českými titulky.
[3]	Internet, webová aplikace Wolfram\|Alpha: Computational Intelligence.
[4]	Internet, Učebnice matematiky — Matematika polopatě.

1 Macron - In Unicode, „combining macron“ is one of the combining diacritical marks, its code is U+0304 (in HTML ̄ or ̄). This (tento) should (měl by) be distinguished (rozeznávat se) from (od) the „macron“ at U+00AF ¯, from (od) the „modifier letter macron“ at U+02C9 ˉ and from (a od) the „combining overline“ at U+0305 ̅. Dále také viz Typografie – skrytá tvář webdesignu » entity.

[ TOP | << | < | > ] notýsek elektronika