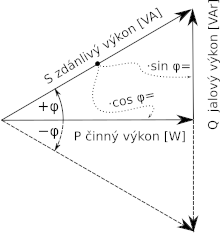
Výkony střídavého proudu, sčítání vektorů.
Rychlé a přehledné poznámky ze základů elektrotechniky doplněné odpovídajícími matematickými vzorci pro orientaci při práci. Má sloužit pro oživení paměti těm, kteří „to už přece znají dávno, ale teď zrovna si nevzpomínají, jak to je přesně, protože to dlouho nepoužívali“ a začínajícím pro „vytvoření si té představy jak to je a poznání mapy elektrotechniky“.

Výkony střídavého proudu, sčítání vektorů.
| výkon zdánlivý (anglicky apparent) |
|
[VA; V, A] | ||||
| výkon činný (anglicky real) (přenáší se ze zdroje do spotřebiče) |
|
[W; V, A] | ||||
| výkon jalový (anglicky reactive) (vyměňuje se mezi reaktivními prvky obvodu) |
|
[VAr; V, A] | ||||
| trojúhelník výkonů |
|
[VA; W, VAr] |
Platí pro ustálený stav a nezkreslený harmonický průběh, jinak nutno zahrnout navíc výkon deformační Pd. Napětí U a proud I jsou v efektivních hodnotách.
| indukované napětí harmonického průběhu |
|
||
| počet závitů na jádru o průřezu SFe v cm2 pro indukované napětí efektivní hodnoty 1 V a harmonickém průběhu o f = 50 Hz a B = 1 T |
;
|
||
| převod transformátoru (závity, napětí,
proudy; indukčnosti, odpory) kde: N … počet závitů, 1 … primární strana, 2 … sekundární strana |
|
||
| přepočet odporů z sekundární na primární stranu |
|
||
| zjištění oteplení transformátoru Δt měřením odporu jeho měděného vinutí, kde R1 … odpor Cu vinutí v chladném stavu, R2 … odpor Cu vinutí v ohřátém stavu, t0 … teplota prostředí na začátku zkoušky, t1 … teplota prostředí na konci zkoušky |
|
Náhradní schéma transformátoru.
R1 — odpor primárního vinutí (činné ztráty v Cu primáru), R21 — odpor sekundárního vinutí přepočítaný na primární stranu (činné ztráty v Cu sekundáru), X1δ — rozptylová reaktance primárního vinutí, X21δ — rozptylová reaktance sekundárního vinutí přepočítaná na primární stranu, Xμ — vazební reaktance magnetizační, RFe — odpor za činné ztráty v železe, U1 — primární napětí, U21 — sekundární napětí přepočítané na primární stranu, Ui1 = Ui21 — indukovaná napětí, I1 — primární proud, I21 — sekundární proud přepočítaný na primární stranu, I0 — proud naprázdno, Iμ — magnetizační proud, IFe — proud na ztráty v železe.
Úměra, která odpovídá skutečným výkonovým
transformátorům:
R1 : R21 : X1δ :
X21δ : Xμ : RFe = 1 : 1 : 2 : 2 :
1 000 : 10 000
| vzájemná (anglicky mutual) indukčnost M |
|
[H; H, H] | ||||
| činitel vazby k, rozsah (0 ≤ k ≤
1), vazba velmi volná k < 0,01, volná k < 0,05, těsná k < 0,9, velmi těsná k > 0,9. |
|
[-; H, H] |
Odjinud: sbírka řešených úloh z fyziky Vzájemná indukčnost cívek, Obvody se vzájemnými indukčnostmi, CÍVKY.
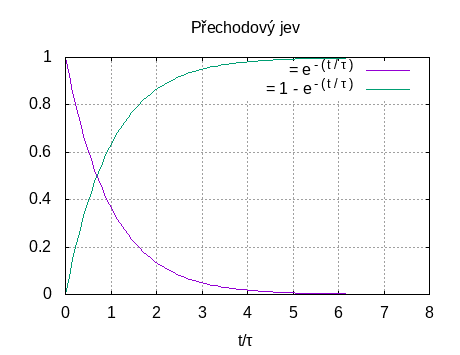
Graf časového průběhu přechodových jevů. Zdrojový text grafu pro gnuplot.
| článek | RC | RL |
|---|---|---|
| časová konstanta (63%; 37%) |
[s; F, Ω] | [s; H, Ω] |
| mezní frekvence (-3dB) | [Hz; F, Ω] | [Hz; H, Ω] |
| integrační | 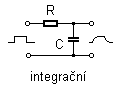 |
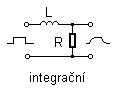 |
| derivační | 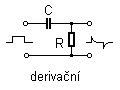 |
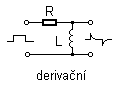 |
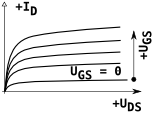
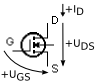
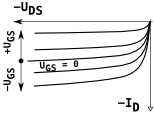
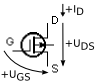
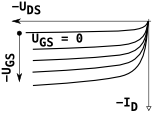
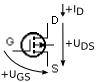
| klasifikace FET-u | stav kanálu při napětí hradla UGS | průběh převodní charakteristiky (Transfer Characteristics) | průběh výstupní charakteristiky | schematická značka | například | ||||
|---|---|---|---|---|---|---|---|---|---|
| oddělení hradla | vodivost kanálu | ovládání kanálu | záporné, UGS < 0 |
nulové, UGS = 0 |
kladné, UGS > 0 |
||||
| MOS-FET MIS-FET izolantem (SiO2) |
N záporné zavírá |
vodivý (ochuzovací, depletion) při nulovém vede |
nevede | vede | vede |  |
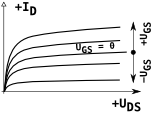 |
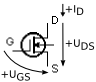 |
TESLA KF520 |
| indukovaný (obohacovací, enhancement) při nulovém nevede |
nevede | nevede | vede |  |
 |
 |
Fairchild Semiconductor IRF520, 2N7000 | ||
| P kladné zavírá |
vodivý (ochuzovací, depletion) při nulovém vede |
vede | vede | nevede |  |
 |
 |
||
| indukovaný (obohacovací, enhancement) při nulovém nevede |
vede | nevede | nevede |  |
 |
 |
|||
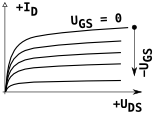
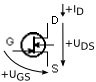
| J-FET PN přechodem, MES-FET Schottkyho přechodem |
N zápornější zavírá |
vodivý (ochuzovací) při nulovém vede |
nevede | vede | nelze |  |
 |
 |
Philips BF245 (J-FET) |
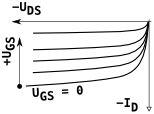
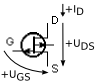
| P kladnější zavírá |
nelze | vede | nevede |  |
 |
 |
|||
| výchozí vztah XL = XC: |
|
[Hz; H, F] | ||||
| vzorec vhodný pro praxi |
|
[MHz; μH, pF] | ||||
| z toho odvozená indukčnost: |
|
[μH; MHz, pF] | ||||
| a nebo odvozená kapacita: |
|
[pF; MHz, μH] |
Teorie: Elektromagnetická forma energie (viz [47]).
Elektrický náboj (Elektrický
náboj – Wikipedie, Elektrický náboj –
Wikina); elementární
částice elektron
(1897, J. J. Thomson) je nositelem kvanta elektrického náboje
−e. El. náboj v klidu nebo pohybu (změna v čase);
energie E (energy) a práce W (work), náboj Q (charge), prostor (rozměr atomů, molekul a
větší): délka l (length), průřez S ((cross-)section) a čas t (time). Dualita
částice a vlnění. Elektromagnetické
pole – Wikipedie; Elektromagnetické
vlny (1832, M. Faraday; 1865, J. C. Maxwell; 1887,
H. Hertz). Klasická elektrodynamika → rok 1900 → kvantová
elektrodynamika (ZE
25 - Elektřina a relativita, ZE
25 - Elektřina a relativita - dojasnění).
Aplikace: elektrotechnika, užito v oborech elektroenergetika (výroba, přenos a užití elektrické energie), elektronika, informační
a komunikační technologie, metalurgie, diagnostika a terapie v lékařství aj.
| složka | ||||||
|---|---|---|---|---|---|---|
proudová  |
elektrická  |
magnetická  |
||||
| činné, mění elektrickou energii na energii tepelnou | reaktivní, akumulující energii | reaktivní, akumulující energii | ||||
| veličina
celková (skalár) |
Elektrický proud | Elektrické napětí | Elektrický indukční tok | Napětí mezi elektrodami | Magnetický indukční tok | Magnetické napětí; Magnetomotorické napětí |
| I [A (Ampér)] I = Q / t |
U [V (Volt)] U = W / Q |
Ψ
= Q [C (Coulomb)] Q = I · t |
U
[V (Volt)] U = W / Q |
Φ
[Wb (Weber)] Φ = W / I |
Um; Fm [A (Ampér)] I = Q / t |
|
| tok, proud | spád, potenciál | tok, proud | spád, potenciál | tok, proud | spád, potenciál | |
| veličina místní (vektor) |
Hustota proudu (skrze plochu) | Intenzita proudového pole (spád el. napětí podél proudové dráhy) | Elektrická indukce (hustota el. indukčního toku skrze plochu) | Intenzita elektrického pole (spád el. napětí podél dráhy) | Magnetická indukce (hustota mag. indukčního toku skrze plochu), [17] | Intenzita magnetického pole (spád mag. napětí podél dráhy) |
| J = I / S [A/m²] | E = U / l [V/m] | D = Ψ / S = Q / S [C/m²] | E = U / l [V/m] | B =
Φ / S
[Wb/m² = T (Tesla)] 1 Gauss = 1 Tesla / 10 000 |
H = Um / l [A/m] | |
| fyzika |
|
|
|
|||
|
Vodič, polovodič, elektrolyt, vakuum; volný nosič náboje; posun náboje v el. poli; náboj v pohybu → el.mag.pole. |
Dielektrikum; elementární el. dipóly, polarizace. Zřídlové, siločára intenzity spojuje místa el. nábojů, zřídlo +Q a propad −Q. Neměnný E⃗ → elektrostatické pole, ΔE⃗ → el.mag. pole. |
Magnetikum; elementární magn. dipóly,
orientace. Vírové,
siločára intenzity
mag. pole je uzavřená křivka bez počátku a konce kolem dráhy spřaženého el. náboje a k ní vždy kolmá; smysl
pravá
ruka. Magnetická složka pole je vzbuzena: |
||||
| Jevy elektromagnetické interakce dějící se v čase a prostoru (rozměr ≥ atomu) vyplněném vakuem nebo látkou (Mendělejevova periodická soustava prvků) v nějakém stavu (T, γ, ε, μ). El. náboj × čas × prostor: nepohybující se → elektrostatické pole; pohybující se → el.mag. pole; neměnný el. proud je stejnosměrný (DC = direct current), měnící se el. proud je střídavý (AC = alternate current). Siločáry jsou ⟂ na ekvipotenciální plochy. | ||||||
| Vliv prostředí pro prostředí lineární a homogenní a izotropní |
||||||
| γ = J / E | ε = D / E | μ = B / H | ||||
| [ Ampér / (Volt × metr) ] | [ Coulomb / (Volt × metr) ] | [ Weber / (Ampér × metr) ] | ||||
| Konduktivita vodiče (měrná elektrická vodivost) γ [gama], schopnost vést el. proud, rezistivita (měrný elektrický odpor ρ [ró]) | Permitivita dielektrika (dielektrická konstanta), schopnost vést el. indukční tok | Permeabilita magnetika (prostředí), schopnost vést mag. indukční tok | ||||
| γ = 1 / ρ | ε = ε0 · εr | μ = μ0 · μr | ||||
| Elektrická susceptibilita | Magnetická susceptibilita | |||||
| Měrná – charakterizuje prostředí (látku, hmotu, materiál) a jeho stav, takže závisí na všem možném, především na teplotě, také na intenzitě, kmitočtu (materiálová disperze) atd. Prostředí lineární/nelineární (stejnoúměrnost), homogenní/nehomogenní (stejnorodost), izotropní/anizotropní (závislost na směru). Citace: „Obecně mohou být ε a μ tenzory druhého řádu … každý reálný materiál vykazuje jistou materiálovou disperzi, díky níž ε nebo μ závisí na frekvenci.“ | ||||||
| Elektrická vodivost, konduktance | Dielektrická vodivost, permitance | Magnetická vodivost, permeance | ||||
| G = γ · (S /
l)
[Siemens = Ampér / Volt] |
Gd = ε · (S / l)
[Farad = Ampér · sekunda / Volt] |
Λ = μ · (S / l)
[Henry = Volt · sekunda / Ampér] |
||||
| Elektrický odpor, rezistance, činný odpor | Dielektrický odpor, elastance | Magnetický odpor, reluktance | ||||
| R = 1 / G [Ω (Ohm)] | Rd = 1 / Gd [1/F] | Rm = 1 / Λ [1/H] | ||||
| Základní vztah: | ||||||
| Ohmův zákon | Hopkinsonův zákon | |||||
| I = U · G = U / R | Ψ = Q = U · Gd | Φ = Um · Λ = Um / Rm | ||||
| Uzavřenou plochou: | ||||||
| 1. Kirchhoffův zákon (uzel) | 2. Kirchhoffův zákon (smyčka) | Gaussova věta | ||||
| I = 0 | U = 0 | Ψ = ΣQ | U = 0 | Φ = 0 | Fm = ΣUm = ΣH · l | |
| Po uzavřené dráze: | Působení elektromagnetického pole; síla, výkon, práce | |||||
|
Jouleovo teplo, magnetické pole, elektrochemické účinky, ionizace. Podle skupenství hmoty:
|
Síla působící na el. náboj, Lorentzova síla Elektrická složka síly na intenzitě elektrického pole E⃗, magnetická složka síly na hustotě magnetického pole B⃗. El. náboj jak se v prostoru pohne, tak magnetuje, dokola kolem sebe kolmo na vektor rychlosti (směr pohybu), což ukazuje výstižný obrázek v článku The Discovery of Radio Waves | Nuts & Volts Magazine. Magn. indukce pohybujícího se el. náboje viz Biotův–Savartův zákon. | |||||
| El. náboje stejné polarity se odpuzují, opačné polarity se přitahují. |
Mag. dipóly se opačnými póly přitahují, shodnými póly se odpuzují.
Směr siločar magnetického toku (orientace elementárních magn. dipólů) vůči směru spřaženého elektrického proudu (el. proud od + pólu k − pólu; tok kladných el. nábojů +Q) podle monsieur André-Marie Ampère pravé ruky. Směr vektoru: ⊗ do nákresny (into page), ⊙ z nákresny (out of page). |
|||||
|
Stejné se odpuzují, opačné přitahují, pravá
ruka, prostorová představa; tato pravidla postačí pro odvození smyslu síly i pro bodový el. náboj i pro vírový magn. dipól, viz následují případy. |
||||||
|
Případ pohybující se el. náboj v el. poli Nepohybující se náboj, síla v rovnováze s G⃗ viz Millikan's Oil drop experiment - Wikipedia. |
Případ pohybující se el. náboj v mag. poli Vždy F⃗ ∟ v⃗ ⇒ rychlost se nemění, mění se směr. Dráha má tvar kružnice, když v⃗ ∟ B⃗, jinak spirála podél Φ s poloměrem podle velikosti B⃗. Proton v magnetickém poli. Vektorový součin, Operace s vektory ×, Operace s vektory +−, Pravidlo pravé ruky. Případ el. proud vodičem v mag. poli
Další jevy spojené s el.mag. polem: Hallův jev – Wikipedie, Skin efekt – Wikipedie. |
|||||
|
Případ dva el. náboje Coulombův zákon – Wikipedie, Coulomb's Law, (podobné jako Newtonův gravitační zákon, The Universal Law of Gravitation). Náboj Q1 v el. poli náboje Q2 a opačně; zřídlové, tvar pole je koule, intenzita elektrického pole z indukce v místě vzdáleném r přes prostředí s ε. |
Případ dva vodiče el. proudu Ampérův silový zákon, dvě magnetická pole V obecném vztahu není vzájemné působení obou proudových elementů symetrické a působící síla obecně není centrální (tj. nepůsobí ve směru spojnice obou elementů). Pro magnetickou sílu proto obecně neplatí zákon akce a reakce. |
|||||
| elektrotechnika | Ideální součástka v obvodu se soustředěnými parametry, která převážně využívá dané složky pole a její význačná a žádaná vlastnost | |||||
| Rezistor: vykazuje elektrický odpor, rezistance/konduktance, činný odpor. Přiváděná elektrická energie je přeměněna na energii tepelnou. Žádanou vlastností je odpor R [Ω], omezením je maximální výkonové zatížení P [W], např. 1 kΩ/6 W. | Kapacitor, kondenzátor: vykazuje odpor zdánlivý kapacitní, kapacitance, kapacitní reaktance/susceptance, viz Imitance. Přiváděná elektrická energie je uložena v elektrickém poli. Žádanou vlastností je kapacita C [F], omezením je maximální přiložené napětí U [V] (nejen), např. 10 μF/16 V. | Induktor, cívka, indukčnost: vykazuje odpor zdánlivý induktivní, induktance, induktivní reaktance/susceptance, viz Imitance. Přiváděná elektrická energie je uložena v magnetickém poli. Zákon elektromagnetické indukce (1831, Michael Faraday), Lenzův zákon (1834, Heinrich Friedrich Emil Lenz). Žádanou vlastností je indukčnost L [H] (vlastní indukčnost, samoindukčnost), omezením je maximální protékaný proud I [A] (nejen), např. 330 μH/5,2 A. | ||||
|
N … počet závitů; Λ … permeance magn. obvodu; AL … cívková konstanta |
||||||
| Představa teorie: ideální součástka, čas, práce. | ||||||
|
Ideální zdroj nastavitelného konstantního proudu nebo napětí. |
Ideální zdroj nastavitelného konstantního proudu, čtyřkvadrantový (spotřebovává z nebo dodává do obvodu el. energii obou polarit), vnitřní odpor Ri = ∞, napětí naprázdno U0 = ∞. Ideální kapacitor, bez ztrát. |
Ideální zdroj nastavitelného konstantního napětí, čtyřkvadrantový (spotřebovává z nebo dodává do obvodu el. energii obou polarit), vnitřní odpor Ri = 0, proud do zkratu Ik = ∞. Ideální induktor, bez ztrát. |
||||
| Ohmův zákon | Zákon elektromagnetické indukce (M. Faraday) | |||||
|
|
||||||
|
Proud vytváří úbytek napětí, napětí protlačí proud. |
Proud přenáší elektrický náboj. Napřed proud pak napětí. |
Indukované napětí brání změně proudu. Napřed napětí pak proud
(cívka jako dívka …). |
||||
|
Práce je objem kvádru napětí krát proud krát čas. |
Práce je polovina objemu kvádru napětí krát proud krát čas. |
Práce je polovina objemu kvádru napětí krát proud krát čas. |
||||
|
|
|
|
||||
| Fázorový diagram ideálního prvku v němž převládá dané pole (složka), zapojeného v obvodu střídavého proudu harmonického průběhu | ||||||
 napětí ve fázi s proudem |
 napětí za proudem |

napětí před proudem |
||||
| Vektory se otáčí rychlostí ω kolem počátku souřadného systému (0, průsečík os). Souřadný systém je pevný, nepohybuje se. Úhel (posunu) od fáze U k fázi I; ČSN EN IEC 60375 ed. 2 - úhel fázového posunu - nlfnorm.cz. | ||||||
| látka | ρ | εr | μr | poznámka |
|---|---|---|---|---|
| [mΩ/(m/mm²)] | [-] | [-] | ||
| vzduch | 1,000 536 | 1,000 000 37 | ||
| voda | 2,27×1014 | 80,37 | 0,999 991 | |
| měď | 17,241 | 0,999 990 | kov, diamagnetický | |
| hliník | 28,74 | 1,000 023 | kov, paramagnetický | |
| polystyren | 2,6 | 1,000 023 |
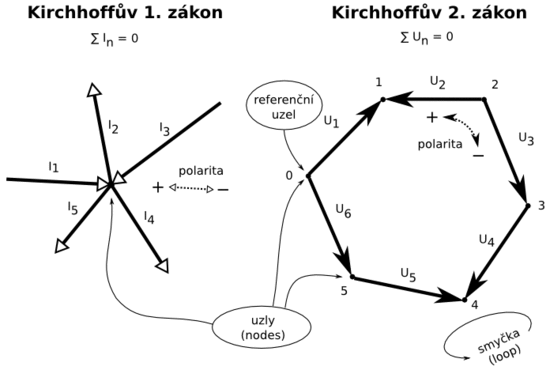
Vyjádření Kirchhoffových zákonů obrázkem. Používáme pro řešení systémů s soustředěnými parametry.
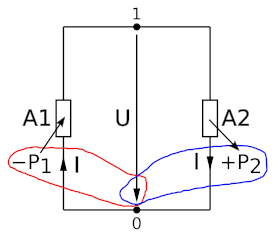
Orientace obvodových veličin, orientace spotřebičová, el. obvod
s prvky s soustředěnými parametry.
V prvku obvodu A1 jsou šipky I a U orientovány proti sobě,
proto je výkon P1 záporný a prvek A1 výkon dodává do
obvodu, je zdrojem (source).
V prvku obvodu A2 jsou šipky I a U
orientovány stejným směrem, proto je výkon P2 kladný a prvek
A2 výkon odebírá z obvodu, je spotřebičem.
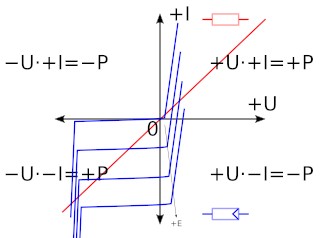
Orientace obvodových veličin, orientace spotřebičová, U-I charakteristika prvku obvodu.
Prvek obvodu se chová jako spotřebič: úsek charakteristiky leží v oblasti, kde P > 0 (+P).
Prvek obvodu se chová jako zdroj: úsek charakteristiky leží v oblasti, kde P < 0 (−P).
Induktor a kapacitor jsou reaktivní prvky, dynamicky přijímají a vrací energii z a do obvodu.
Řešení lineárních el. obvodů viz Superpozice (elektrotechnika) – Wikipedie ; napěťové zdroje (Ri = 0) se zkratují a proudové zdroje (Ri = ∞) se rozpojí. ČSN EN IEC 60375 ed. 2 - ideální napěťový zdroj - nlfnorm.cz, ČSN EN IEC 60375 ed. 2 - ideální zdroj proudu - nlfnorm.cz, ČSN EN IEC 60375 ed. 2 - Kirchhoffův zákon o proudech v uzlu - nlfnorm.cz, ČSN EN IEC 60375 ed. 2 - Kirchhoffův zákon o napětích ve smyčce - nlfnorm.cz.
Imitance je společný název
pro impedanci (zdánlivý odpor) v Ω (Ohm) a admitanci (zdánlivá vodivost) v S
(Siemens).
impedance² = rezistance² + reaktance² ; admitance²
= konduktance² + susceptance² .
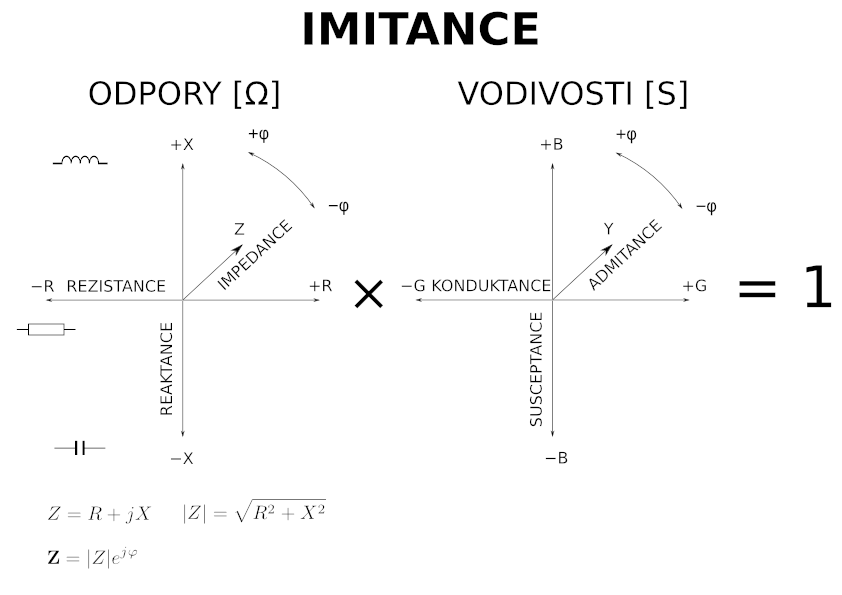
Imitance – přehled.
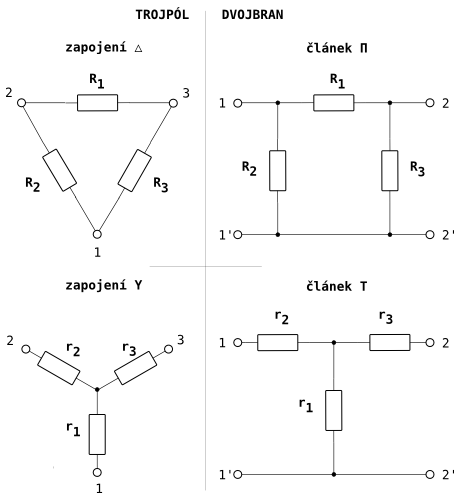
Zapojení do hvězdy, do trojúhelníka; článek Π článek T.
Přepočet z trojúhelníka na hvězdu:
Přepočet z hvězdy na trojúhelník:
Výpočet útlumového článku skriptem Resistive Pads na stránkách VK2ZAY, Fixed Pi & T Attenuators - Equations - RF Cafe, nebo tabulkou viz Appendix 3 v [21], Compute Low-Frequency Parameters of Resistive Attenuators with Three DC-Resistance Measurements.
Zdroje informací, které stojí za to:
| [1] | L. Javorský, A. Bobek, R. Musil, kniha Základy elektrotechniky pro střední průmyslové školy elektrotechnické, SNTL Praha 1970. |
| [2] | Ing. Jan Maťátko, kniha, ELEKTRONIKA, IDEA SERVIS 2002. |
| [3] | Kolektiv ÚFI FSI VUT v Brně , kniha Elektřina a magnetismus. Věnováno všem, kteří mají zájem o fyziku a její radostné studium. |
| [4] | Tony R. Kuphaldt, Internet Lessons In Electric Circuits. A free series of textbooks on the subjects of electricity and electronics. |
| [5] | Tony R. Kuphaldt, Internet All About Circuits : Free Electric Circuits Textbooks. This site provides a series of online textbooks covering electricity and electronics. |
| [6] | Jaroslav Reichl, Martin Všetička, Internet, Encyklopedie fyziky. Encyklopedie fyziky vydávaná formou průběžně aktualizovaných webových stránek. |
| [7] | David W. Knight, G3YNH, AC electrical theory. An introduction to Phasors, Impedance and Admittance. Výborně doplňuje učebnice Základy elektrotechniky [1] a Elektronika [2]. Také Electrical Theory, Components and Materials, Impedance Matching. Part 1: Basic Principles. a další! |
| [8] | Edmund A. Laport, Radio Antenna Engineering - kniha z roku 1952. Elektronická edice v souboru RadioAntennaEngineering-ebook.pdf, RadioAntennaEngineering-ebook.pdf o velikosti cca 25 MB ve formátu pdf. |
| [9] | Paul Horowitz, Winfield Hill; THE ART OF ELECTRONICS; překlad do ruštiny П.Хоровиц, У.Хилл; ИСКУССТВО СХЕМОТЕХHИКИ; 1-й том (5mb) a 2-й том (5,6mb), původní odkazy jsou na stránce Библиотека радиолюбителя. |
| [10] | Ing. Josef Říha, kniha, Elektrické stroje a přístroje, SNTL Praha 1986. |
| [11] | OK2BUH, Internet, Seriál na pokračování: Antény a impedance. |
| [12] | Rostislav Wasyluk, kniha, ELEKTROTECHNOLOGIE pro školu a praxi, Scientia spol. s r. o. 2004. |
| [13] | Richard Fitzpatrick, Internet, Classical Electromagnetism: An intermediate level course. |
| [14] | Zbyněk Raida, Dušan Černohorský, Dalimil Gala, Stanislav Goňa, Zdeněk Nováček, Viktor Otevřel, Václav Michálek, Vlastimil Navrátil, Tomáš Urbanec, Zbyněk Škvor, Petr Poměnka, Jiří Šebesta, Geert Vanderstegen, Bart Vandijck, Bert Soors, Jeroen Schevernels, Javier Martín del Valle, Martin Štumpf, Vladimír Šeděnka, Peter Kovács, Jaroslav Láčík, Jana Jilková, Zbyněk Lukeš, Michal Pokorný, Internet, multimediální učebnice Elektromagnetické vlny, Mikrovlnná technika. |
| [15] | Petr Schovánek, Vítězslav Havránek, Internet, Chyby a nejistoty měření (doplňující text k laboratornímu cvičení). |
| [16] | Lubomír Ivánek, Internet, ELEKTROMAGNETISMUS, prezentace Základní pojmy. |
| [17] | Hubeňák J., Internet, Měření magnetické indukce, PDF ke stažení. |
| [18] | Václav Žalud, kniha Moderní radioelektronika, nakladatelství BEN – technická literatura, Praha 2000. |
| [19] | Prof. Ing. Daniel Mayer, DrSc., kniha Úvod do teorie elektrických obvodů, SNTL/ALFA, Praha 1981. |
| [20] | Analog Engineer’s Pocket Reference. |
| [21] | Ian Hickman BSc (Hons), CEng, MIEE, MIEEE, Practical Radio-Frequency Handbook. |
| [22] | Keysight Technologies, Application Note Impedance Measurement Handbook; A guide to measurement technology and techniques 6th Edition. |
| [23] | Ing. Petr Vavřiňák, Základy elektrotechniky – řešení příkladů: Střídavé proudy;. |
| [24] | Překlad kurzu Elektřina a magnetizmus z MIT, MIT: Elektřina a magnetizmus na serveru aldebaran.cz. |
| [25] | TUL, Martin Černík, Elektrické obvody: teorie a příklady. |
| [26] | Indukčnost – Wikipedie. |
| [27] | Is Time a Vector or a Scalar? (The Answer May Surprise You!) - Profound Physics. |
| [28] | A.T. Starr; Electric Circuits and Wave Filters. |
| [29] | záznam přednášky Jiří Podolský - Od hmotných bodů ke spojitým polím (MFF FJDP 15.3.2018). |
| [30] | Wavelength - Wikipedia. Stojatá vlna nejnázornější; teprve animací se znázorní čas a stojatá opravdu stojí a dvojnásobně namáhá stejná místa. |
| [31] | The Discovery of Radio Waves | Nuts & Volts Magazine. |
| [32] | The speed limit of optoelectronics | Nature Communications. |
| [33] | Internet, Mapa fyziky. Anglicky, s českými titulky. |
| [34] | Internet, Fyzika, o které se raději nemluví - YouTube. |
| [35] | Internet, Physics - Stellar Atmospheres, Celestial Mechanics, Classical Mechanics, Geometric Optics, Electricity and Magnetism, Heat and Thermodynamics, Planetary [APhotometry. |
| [36] | Internet, 7.3 Vedení proudu v pevných látkách. |
| [37] | Internet, Matej Halouska, Fyzikální veličiny a jejich jednotky - přehledná tabulka. |
| [38] | Internet, Textbook for Electrical Engineering & Electronics. |
| [39] | Internet, Maxwell's Equations. |
| [40] | Internet, A Visual Introduction to Scattering Parameters. |
| [41] | Internet, Physics 43 Magnetic Forces on Moving Charges (17 of 26) Thompson's e/m Ratio - YouTube. |
| [42] | Internet, Lec 05: Electrostatic Shielding (Faraday Cage) | 8.02 Electricity and Magnetism (Walter Lewin) - YouTube. |
| [43] | Internet, Základy elektrotechniky na stránkách SPŠE Mohelnice © Jozef Diviš. |
| [44] | Internet, Základy elektroniky na stránkách SPŠE Mohelnice, © Jozef Diviš. |
| [45] | TECHNICKÁ UNIVERZITA V LIBERCI, Martin Černík, Elektrické obvody: teorie a příklady. |
| [46] | Internet, Názorná elektrotechnika - Kurz základů elektrotechniky od samouka pro samouky; Základy Elektrotechniky. |
| [47] | Internet, FyzWeb - síly; mapa. |
| [48] | Internet, ACoC 2025: Day 4: Magnetic Material Investigation Apparatus; ACoC 2025: Day 7: Barkhausen Noise - YouTube; Barkhausen effect - Wikipedia. |